读书笔记:Javascript函数式编程指南（二）

本博客 hjy-xh，转载请申明出处

今日分享: 如何创建易于推断的代码

轻数据结构，重操作

理解程序中控制流

程序为实现业务目标所要进行的路径被成为控制流。 命令式程序需要通过暴露所有的必要步骤才能极其详细地描述其控制流。这些步骤通常涉及大量的循环和分支，以及随语句执行变化的各种变量。

简单的命令式程序大致可以这样描述:

var loop = optC();
while (loop) {
  var condition = optA();
  if (condition) {
    optB1();
  } else {
    optB2();
  }
  loop = optC();
}
optD();

如下图所示：

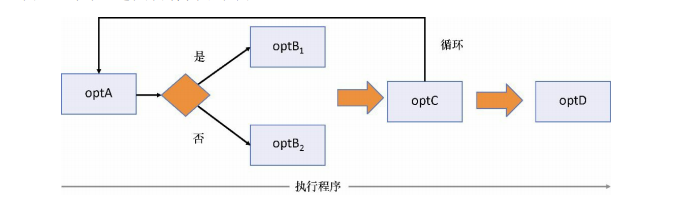
然而，声明式程序，特别是函数式程序，则多使用以简单拓扑连接的独立黑盒操作组合而成的较小结构化控制流，从而提升程序的抽象层次。

这些连接在一起的操作只是一些能够将状态传递至下一个操作的高阶函数，如下图所示。使用函数式开发风格操作数据结构，其实就是将数据与控制流视为一些高级组件的简单连接。

使用这种方式可以形成类似这样的代码：

optA().optB().optC().optD();

采用这种链式操作能够使程序简洁、流畅并富有表现力，能够从计算逻辑中很好地分离控制流，因此可以使得代码和数据更易推理。

链接方法

方法链是一种能够在一个语句中调用多个方法的面向对象编程模式。当这些方法属于同一个对象时，方法链又称为方法级联。

尽管该模式大多出现在面向对象的应用程序中，但在一些特定条件下，如操作不可变对象时，也能很好地用于函数式编程中。

既然在函数式代码中是禁止修改对象的，又如何能使用这种方法链模式呢？让我们来看一个字符串处理的例子：

"Functional Programming".substring(0, 10).toLowerCase() + " is fun";

在这个中，substring 和 toLowerCase 都是（通过 this）在隶属的字符串对象上操作并返回一个新字符串的方法。JavaScript 中字符串的加号（+）运算符被重载为连接字符串操作的语法糖，它也会返回一个新的字符串。通过一系列变换后的结果与原先字符串毫无引用关系，而原先的字符串也不会有任何变化。

这种行为是理所当然的，因为按照设计，字符串是不可变的。从面向对象的角度来看，这没有什么特别的。但从函数式编程的角度来看，这是一种理想行为。

如果用更加函数式的风格重构上面的代码，它会像这样：

concat(toLowerCase(substring('Functional Programming', 1, 10))),' is fun');

这段代码符合函数式风格，所有参数都应在函数声明中明确定义，而且它没有副作用，也不会修改的原有对象。

但可以说，这样的代码写起来并没有方法链流畅。而且它也更难阅读，因为需要一层层地剥离外部函数，才能知晓内部真正发生的事情。

只要遵守不可变的编程原则，函数式中也会应用这种隶属于单个对象实例的方法链。能用该模式来处理数组变换吗？

函数链

面向对象程序将继承作为代码重用的主要机制。子类继承了父类的所有状态和方法，例如在 Java 中，有一大堆继承于基础接口 List 的各种实体 List 类，如 ArrayList、LinkedList、DoublyLinkedList、CopyOnWrite ArrayList 等，它们都源自共同的父类，并各自添加了一些特定的功能。

函数式编程则采用了不同的方式。它不是通过创建一个全新的数据结构类型来满足特定的需求，而是使用如数组这样的普通类型，并施加在一套粗粒度的高阶操作之上，这些操作是底层数据形态所不可见的。

这些操作会作如下设计:

• 接收函数作为参数，以便能够注入解决特定任务的特定行为。

• 代替充斥着临时变量与副作用的传统循环结构，从而减少所要维护以及可能出错的代码。

继续之前，我们先看一些东西并暂时记住它

// Person class
class Person {
  constructor(firstname, lastname, ssn) {
    this._firstname = firstname;
    this._lastname = lastname;
    this._ssn = ssn;
    this._address = null;
    this._birthYear = null;
  }
  get ssn() {
    return this._ssn;
  }
  get firstname() {
    return this._firstname;
  }
  get lastname() {
    return this._lastname;
  }
  get address() {
    return this._address;
  }
  get birthYear() {
    return this._birthYear;
  }
  set birthYear(year) {
    this._birthYear = year;
  }
  set address(addr) {
    this._address = addr;
  }
  toString() {
    return `Person(${this._firstname}, ${this._lastname})`;
  }
}

const p1 = new Person("Haskell", "Curry", "111-11-1111");
p1.address = new Address("US");
p1.birthYear = 1900;

const p2 = new Person("Barkley", "Rosser", "222-22-2222");
p2.address = new Address("Greece");
p2.birthYear = 1907;

const p3 = new Person("John", "von Neumann", "333-33-3333");
p3.address = new Address("Hungary");
p3.birthYear = 1903;

const p4 = new Person("Alonzo", "Church", "444-44-4444");
p4.address = new Address("US");
p4.birthYear = 1903;

lambda 表达式

lambda 表达式（在 JavaScript 中也被称为箭头函数）源自函数式编程，比起传统的函数声明，它可以采用相对简洁的语法形式来声明一个匿名函数。

尽管 lambda 函数也可以写成多行形式，但单行是最普遍的形式。使用 lambda 表达式或普通函数声明语法一般只会影响到代码的可读性，其本质是一样的。

下面是一个可用于提取个人姓名的示例函数：

const name = (p) => p.fullname;
console.log(name(p1)); //-> 'Haskell Curry'

(P) => p.fullname 这种简洁的语法糖表明它只接收一个参数 p 并隐式地返回 p.fullname。

lambda 表达式适用于函数式的函数定义，因为它总是需要返回一个值。对于单行表达式，其返回值就是函数体的值。

另一个值得注意的是一等函数与 lambda 表达式之间的关系。函数名代表的不是一个具体的值，而是一种（惰性计算的）可获取其值的描述。换句话说，函数名指向的是代表着如何计算该数据的箭头函数。这就是在函数式编程中可以将函数作为数值使用的原因。
之后会深入讨论惰性计算函数。

很多函数式的 JavaScript 代码都需要处理数据列表，这也就是衍生 JavaScript 的函数式语言鼻祖起名为 LISP（列表处理）的原因。JavaScript 5.1 本身就提供特定版本的该类操作——称为函数式array extras,也就是forEach、map``reduce 以及 filter 这些函数，它们都能够与 lambda 表达式良好地配合使用。

代码推理

“代码推理”到底是什么意思呢？

之前的章节用“松散”这个词来表征分析一个程序任何一个部分，并建立相应心智模型的难易程度。

该模型分为两部分：动态部分包括所有变量的状态和函数的输出，而静态部分包含可读性以及设计的表达水平。

两个部分都很重要。不可变性和纯函数会使得该模型的构建更加容易。之前的内容强调将高阶操作链接起来构成程序的价值。

命令式的程序流与函数式的程序流有着本质的不同。函数式的控制流能够在不需要研究任何内部细节的条件下提供该程序意图的清晰结构，这样就能更深刻地了解代码，并获知数据在不同阶段是如何流入和流出的。

声明式惰性计算函数链

之前提到，函数式程序是由一些简单函数组成的，尽管每个函数只完成一小部分功能，但组合在一起就能够解决很多复杂的任务。

函数式编程的声明式模型将程序视为对一些独立的纯函数的求值，从而在必要的抽象层次之上构建出流畅且表达清晰的代码。这样就可以构成一个能够清晰表达应用程序意图的本体或词汇表。使用如map、reduce 和 filter 这样的基石来搭建纯函数，可使代码易于推理并一目了然。

这个层次的抽象的强大之处在于，它会使开发者开始认识到各种操作应该对所采用的底层数据结构不可见。从理论上说，无论是使用数组、链表、二叉树还是其他数据结构，它都不应该改变程序原本的语义。正是出于这个原因，函数式编程选择更关注于操作而不是数据结构。

例如，假设需要对一组姓名进行读取、规范化、去重，最终进行排序。首先写一个命令式的版本，然后再重构成函数式的风格。

const names = [
  "alonzo church",
  "Haskell curry",
  "stephen_kleene",
  "John Von Neumann",
  "stephen_kleene",
];

let result = [];
for (let i = 0; i < names.length; i++) {
  //<--- 遍历数组中的所有名字
  let n = names[i];
  if (n !== undefined &amp;&amp; n !== null) {
    //<--- 检查所有词是否都合法
    let ns = n.replace(/_/, " ").split(" "); //<--- 数组包含格式不一致的数据。这是规范化（修复）元素的步骤
    for (let j = 0; j < ns.length; j++) {
      let p = ns[j];
      p = p.charAt(0).toUpperCase() + p.slice(1);
      ns[j] = p;
    }
    if (result.indexOf(ns.join(" ")) < 0) {
      //<--- 检查是否已存在于结果中，以去除重复的元素
      result.push(ns.join(" "));
    }
  }
}
result.sort(); // <--- 数组排序

命令式代码的缺点是限定于高效地解决某个特定的问题。例如，这段代码用于解决上述的问题。比起函数式代码，其抽象水平要低得多。抽象层次越低，代码重用的概率就会越低，出现错误的复杂性和可能性就会越大。此外，函数式的实现不过是将各种黑盒组件连接在一起，将重任赋予如map、reduce 和 filter这些成熟且经过测试的 API。请注意，级联排列的函数调用可以使该代码更易阅读。

_.chain(names) //<--- 初始化函数链（创建惰性计算函数链来处理给定的数组）
  .filter(isValid) //<--- 去除非法值
  .map((s) => s.replace(/_/, " ")) //<--- 规范化值
  .uniq() <
  ---去掉重复元素
    .map(_.startCase) //<--- 大写首字母
    .sort()
    .value(); //<--- 执行函数链中的所有函数
//-> ['Alonzo Church', 'Haskell Curry', 'Jon Von Neumann', 'Stephen Kleene']

这样的代码看起来舒服很多，不仅是因为代码量的减少，还因为其结构简单明了。

现在我们可以更深刻明白为什么函数式的程序是如此优越。能够写得如此流畅与函数式编程中的纯性以及无副作用的基本原则息息相关。链中的每个函数都以一种不可变的方式来处理由上一个函数构建的新数组。Lodash 利用函数链这种模式，通过调用_.chain()提供了一种基础功能，以满足各种需求。这有助于过渡到对 point-free 编程风格的理解。pointfree 是函数式编程的特色，会在之后分享。

能够惰性地定义程序的管道不止有可读性这一个好处。由于以惰性计算方式编写的程序会在运行前定义好，因此可以使用数据结构重用或者方法融合等技术对其进行优化。这些优化不会减少执行函数本身所需的时间，但有助于消除不必要的调用。之后会更详细解释。

类 SQL 的数据：函数即数据

比如map、reduce、filter等。将这些函数组成一个列表，可用来梳理数据相关的信息。如果在更高层面细细思考，就会发现这些函数与SQL相似，这不是偶然的。

SELECT p.firstname, p.birthYear FROM Person p
WHERE p.birthYear > 1903 and p.country IS NOT 'US'
GROUP BY p.firstname, p.birthYear

事实证明，在构建程序时，使用查询语言来思考与函数式编程中操作数组类似——使用通用关键字表或代数方法来增强对数据及其结构的深层次思考。

Lodash 支持一种称为 mixins 的功能，可以用来为核心库扩展新的函数，并使得它们可以以相同的方式连接：

_.mixin({
  select: _.pluck,
  from: _.chain,
  where: _.filter,
  groupBy: _.sortByOrder,
});

编写类似 SQL 的 JavaScript 代码:

_.from(persons)
  .where((p) => p.birthYear > 1900 && p.address.country !== "US")
  .groupBy(["firstname", "birthYear"])
  .select("firstname", "birthYear")
  .value();
//-> ['Alan', 'Barkley', 'John']

上面的代码创建了一个 SQL 关键字到对应别名函数的映射，从而可以更深刻地理解一个查询语言的函数式特性。

递归

另一种用于替换循环的常见技术是递归，尤其当处理一些“自相似”的问题时，可以用其来抽象迭代。对于这些类型的问题，序列函数链会显得效率低下或不适用。而递归实现了自己的处理数据的方式，从而大大缩短了标准循环的执行时间。

在 JavaScript 中，递归具有许多应用场景，例如解析 XML、HTML 文档或图形等。

什么是递归？

递归是一种旨在通过将问题分解成较小的自相似问题来解决问题本身的技术，将这些小的自相似问题结合在一起，就可以得到最终的解决方案。递归函数包含以下两个主要部分。

• 基例（终止条件）
• 递归条件

基例是能够令递归函数计算出具体结果的一组输入，而不必再重复下去。递归条件则处理函数调用自身的一组输入（必须小于原始值）。如果输入不变小，那么递归就会无限期地运行，直至程序崩溃。

随着函数的递归，输入会无条件地变小，最终到达触发基例的条件，以一个值作为递归过程的终止。

栗子：递归求和

function sum(arr) {
    if(_.isEmpty(arr)) { <---//  基例（终止条件）
        return 0;
    }
    return _.first(arr) + sum(_.rest(arr)); //<--- 递归条件：使用更小一些的输入集调用自身。这里通过_.first和_.rest缩减输入集
}
sum([]); //-> 0
sum([1,2,3,4,5,6,7,8,9]); //->45

递归定义的数据结构

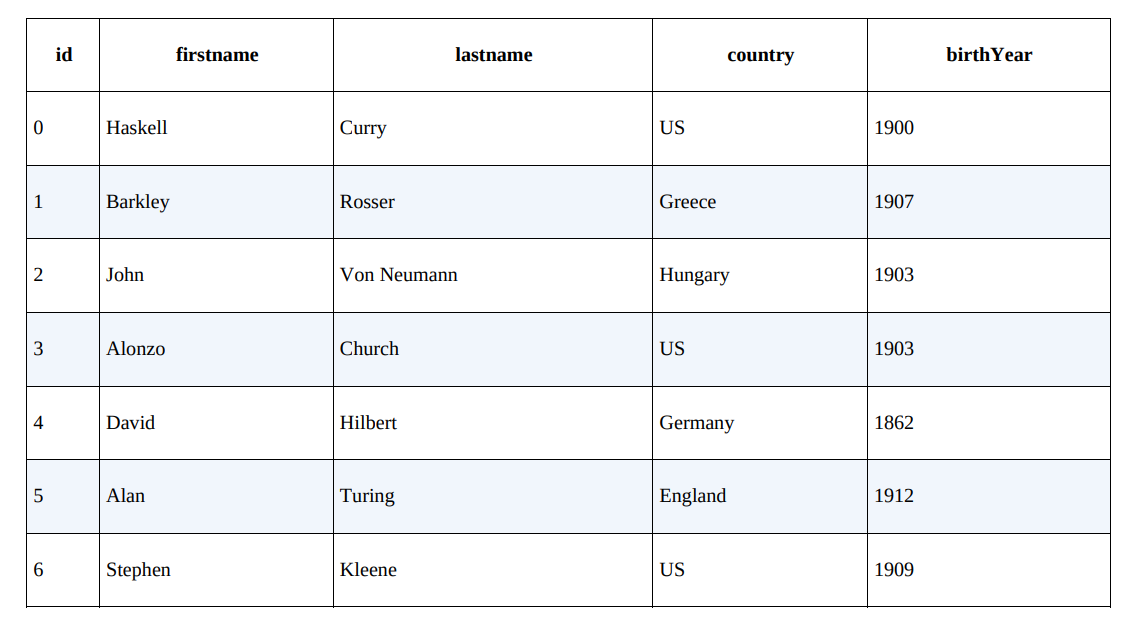
person 对象示例数据中的那些名字。20 世纪 20 年代，函数式编程（lambda 演算、范畴论等）背后的数学社区非常活跃。大部分发表的研究成果都是融合一些由 Alonzo Church 这样的知名大学教授提出的思想和定理。事实上，许多数学家，如 Barkley Rosser、Alan Turing 和 Stephen Kleene 等，都是 Church 的博士生。后来他们也有了自己的博士生。下图为这种师徒关系（的一部分）的示意图。

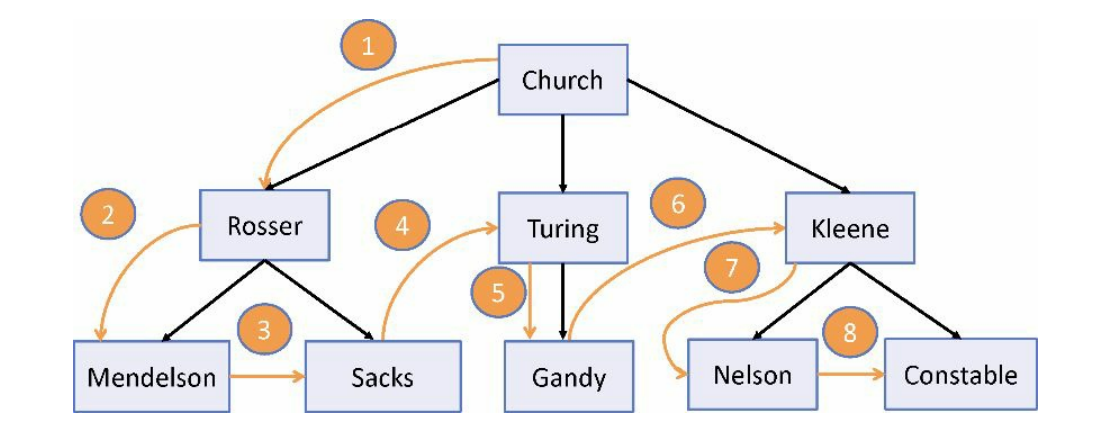
这种结构在软件中是很寻常的，它可用于建模 XML 文档、文件系统、分类法、种别、菜单部件、逐级导航、社交图谱等，所以学习如何处理它们至关重要。图 3.8 显示了一组节点，其连线表示了导师-学生这一关系。到目前为止，我们已经利用函数式技术解析过一些扁平化的数据结构，如数组。但这些操作对树形数据是无效的。因为 JavaScript 没有内置的树型对象，所以需要基于节点创建一种简单的数据结构。节点是一种包含了当前值、父节点引用以及子节点数组的对象。

节点对象的定义

class Node {
    constructor(val) {
        this._val = val;
        this._parent = null;
        this._children = [];
    }
    isRoot() {
        return isValid(this._parent); <--- 之前创建的函数
    }
    get children() {
        return this._children;
    }
    hasChildren() {
        return this._children.length > 0;
    }
    get value() {
        return this._val;
    }
    set value(val) {
        this._val = val;
    }
    append(child) {
        child._parent = this; //<--- 设置父节点
        this._children.push(child); //<--- 将孩子节点加入孩子列表中
        return this; //<--- 返回该节点（便于方法级联）
    }
    toString() {
        return `Node (val: ${this._val}, children: ${this._children.length})`;
    }
}

可以这样创建一个新节点：

const church = new Node(new Person("Alonzo", "Church", "111-11-1111")); // <--- 重复树中的所有节点

树是包含了一个根节点的递归定义的数据结构：

class Tree {
  constructor(root) {
    this._root = root;
  }
  static map(node, fn, tree = null) {
    //<--- 使用静态方法以免与Array.prototype.map 混淆。静态方法也能像单例函数一样高效
    node.value = fn(node.value); //<--- 调用遍历器函数，并更新树中的节点值
    if (tree === null) {
      tree = new Tree(node); //<--- 与 Array.prototype.map 类似。结果是一个新的结构
    }
    if (node.hasChildren()) {
      //<--- 如果节点没有孩子，则返回（基例）
      _.map(node.children, function (child) {
        //<--- 将函数应用到每一个孩子节点
        Tree.map(child, fn, tree); //<--- 递归地调用每一个孩子节点
      });
    }
    return tree;
  }
  get root() {
    return this._root;
  }
}

节点的主要逻辑在于 append 方法。要给一个节点追加一个子节点，需要将该节点设置为子节点的 parent 引用，并把子节点添加至该节点的子节点列表中。通过从根部不断地将节点链接到其他子节点来填充一棵树，由 church 开始：

church.append(rosser).append(turing).append(kleene);
kleene.append(nelson).append(constable);
rosser.append(mendelson).append(sacks);
turing.append(gandy);

每个节点都包裹着一个 person 对象。递归算法执行整个树的先序遍历，从根开始并且下降到所有子节点。由于其自相似性，从根节点遍历树和从任何节点遍历子树是完全一样的，这就是递归定义。为此，可以使用与 Array.prototype.map 语义类似的高阶函数 Tree.map——它接收一个对每个节点求值的函数。可以看出，无论用什么数据结构来建模（这里是树形数据结构），该函数的语义应该保持不变。从本质上讲，任何数据类型都可以使用 map 并保持其结构不变。

树的先序遍历按照以下步骤执行，从根节点开始。

• 显示根元素的数据部分。
• 通过递归地调用先序函数来遍历左子树。
• 以相同的方式遍历右子树。

下图显示了算法采用的路径：

函数 Tree.map 有两个必需的输入：根节点（即树的开始）以及转换每个节点数值的迭代函数：

Tree.map(church, (p) => p.fullname);

它以先序方式遍历树，并将给定的函数应用于每个节点，输出以下结果：

'Alonzo Church', 'Barkley Rosser', 'Elliot Mendelson', 'Gerald Sacks', 'Alan
Turing', 'Robin Gandy', 'Stephen Kleene', 'Nels Nelson', 'Robert Constable'

总结

• 使用map、reduce和filter等高阶函数来编写高可扩展的代码。
• 使用 Lodash 进行数据处理，通过控制链创建控制流与数据变换明确分离的程序。
• 使用声明式的函数式编程能够构建出更易理解的程序。
• 将高阶抽象映射到 SQL 语句，从而深刻地认识数据。
• 递归能够解决自相似问题，并解析递归定义的数据结构。